
Volcanoes send large amount of ash higher up into the stratosphere, along with gases that chemically react to form additional lingering aerosols. These aerosols scatter additional light along the grazing ray paths, reducing the umbral illumination. Increasing darkness of the eclipsed moon thus acts as a gauge that measures the amount of volcanic aerosols in the stratosphere. The appearance and colors in the umbra really provide a sort of mirror showing what is happening in various layers of the atmosphere here on Earth. Beyond the volcanic effects, it's interesting to note that near the edge of the umbra the light rays only pass higher up in the stratosphere and switch to a more bluish color where absorption by the ozone layer predominates.
Back in 1994 I developed a ray-tracing program that refracts rays from the sun through the Earth's atmosphere to illuminate the moon during a lunar eclipse. Images of the moon can be produced in this way. Just recently in 2015 I picked up on this project to further test and develop this software. The animation below shows the moon during various times for the September 27-28 2015 total lunar eclipse. The first eight frames are between 2nd and 3rd contact (using a constant brightness setting). The last two are after 3rd contact and have the brightness lowered to prevent image saturation. North is up. (Click on the image for a larger version).
A linear (gamma corrected) brightness is displayed to provide realistic contrast. More details will show if viewed full screen with monitor brightness turned up. A reflectance map of the moon has been added so we can see the Maria and such.
The software is using simple representation of clouds along the terminator. Ozone absorption is now being included, using a uniform value of 280 Dobson units. A future enhancement would be to make this ozone abundance vary with latitude. Stratospheric aerosols are included here with an optical depth of .01. The simulated image is nicely sensitive to the values of both ozone and aerosols. Volcanic twilights were present and the associated aerosols appear to have darkened this eclipse based on my recent visual eclipse observations. The simulation suggests that the eclipse at mid-totality was darkened about 0.4 magnitude. This is also borne out in Rich Keen's analysis.
With the various assumptions in the model we can come up with an apparent magnitude of -1.7 at mid-eclipse. This is based on the V-band and a correction would be needed to account for the excess brightness of the moon in red light (and a deficiency in blue light). Thus the color corrected apparent magnitude would be somewhat different though I'm unsure exactly how much and in what direction. Additional details on each frame can be seen in this log file.
Note that I believe that the uneclipsed full moon has a magnitude about 0.18 brighter than usually cited because the opposition effect is very strongly peaked around 0 degrees phase angle and this peak is only partially included in the widely adopted lunar magnitude forumlae.
Solar limb darkening is being accounted for.

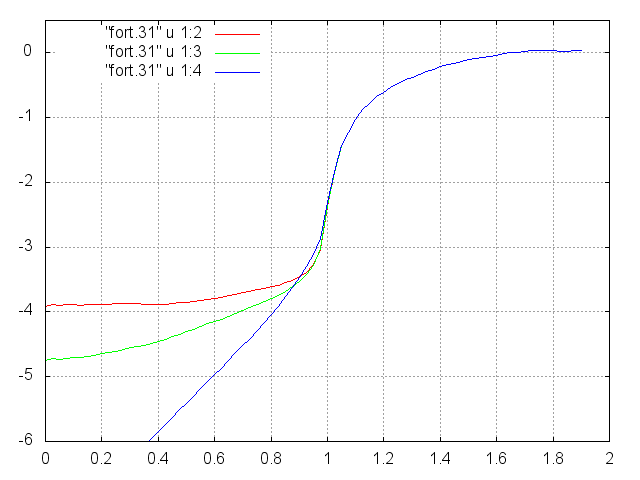
Fig 1. The above left image (1a - click on it) shows a comparison of a partial eclipse with and without the atmosphere.
The above right image (1b - click on it) shows a plot of log shadow intensity (vertical axis) vs. distance from the center of the umbra (horizontal axis). Wavelengths corresponding to red, green, and blue are shown. The blinking comparison illustrates the effect of the Earth's atmosphere.
The shapes of these curves are close to what we see in references [2,3,4].
At least that's what the model is showing so far. It is suggested in "Celestial Shadows" [5] that the ozone layer absorption is responsible for the umbral enlargement, yet this is much lower than the notional eclipsing layer of around 85km [6]. It may be possible to do a model run without ozone and see if it changes the inflection point. Refraction is also very small at this altitude. The notional eclipsing layer may be about twice as high as the actual region of direct atmospheric effects (i.e. atmospheric absorption and refraction). The resulting high altitude of the notional layer may have to do with the diminishing returns of the small solar crescent competing with the sum total of all the light that is refracted through the atmosphere.
The assumption is being made that contrast perception is based on changes in logarithmic brightness. There is an interesting discussion of this in reference [7]. Whether this affects where we see the umbra edge may be a consideration.
I'm starting to make animations of how things look from a vantage point on the lunar surface. (Click for a larger version)

To deal with the brightness range, during the partial eclipse and shallow total eclipse (as seen from this point on the moon) the brightness is scaled so that 255 is the surface brightness of the center of the sun. The brightness is increased as our viewing position approaches the center of the umbra up to a factor of 70 (beginning of animation). The animation begins with the viewer at the center of the umbra and the ring has a visual magnitude of about -15. This brightens to -20 at the umbra's edge and up to -27 when the sun fully emerges.
The solar corona is relatively much dimmer than the rest of the scene being shown. It seems it would barely register more than a count or two unless the brightness scale is cranked up further.
I like to view these animations full screen with the monitor brightness turned up. The view might resemble wearing sunglasses or a solar filter depending on the stage of the eclipse. Even in deep totality the surface brightness could be fairly bright in spots, kind of like a sunset on Earth. I'm presently assuming clean air so adding tropospheric aerosols may dim things a bit more when we're in deep totality.
It's interesting to see a somewhat different presentation in this actual Kaguya movie, as explained in this press release. This is an (even more) unusual situation with the brightness turned up more than in my animation, viewed by Kaguya while significantly outside the edge of the umbra. The bright part of the sun is initially hidden by Earth/Sun rise on the moon's limb. We are seeing a more complete blue/white ring in the video at this stage than in my animation. This may be from scattered light in Earth's atmosphere (instead of pure refraction), and isn't yet included in this model as in more "normal" situations it would be rather faint to see next to the brighter sun. It maybe could be added in for completeness on the low end of the brightness scale or in 16-bit imagery.
I think there's a better match to some of the Surveyor eclipse imagery (bottom of link).
The above model was developed independently from my other "all-sky" software. Recently the all-sky model was improved to show a similar view, here we see a zoom in on the Earth's limb. The 16K cropped animation starts just within the umbra and we progress through the center of the umbra during the sequence. The upper limb of the apparent (refracted) sun slowly sinks as the actual solar limb goes farther down below the Earth's limb. (Click for a larger version)
Just prior to the animation, when the actual sun and Earth limb concide, the apparent sun reaches around 35km off the limb. One definition of the umbral edge and notional eclipsing layer would be when the angular velocity of the apparent sun is half the true angular velocity. By my initial calculation, this happens when the true sun is about 34km up and the apparent is 47km. The velocities get within about 10% of each other when the respective limbs are 70km and 71km up. Here is a table of the actual and apparent values.
Actual Apparent ------ -------- 0km 35km 26km 43km 42km 51km 55km 59km 65km 67km 74km 75km
Near the end of the animation when the center of the sun goes enough below the Earth's center the ring disappears completely. The scattered light of the blue sky is barely visible given the "exposure" settings that are designed to show the sun without washing out its colors.
Here is a full disk 4K animation. Deeper into the umbra red arcs of sunlight refracted through the lower troposphere dance along the limb in locally clear areas between clouds rotating in and out of view. I'd recommend turning up your monitor brightness for best viewing.
Space artist Don Davis made a really nice video showing a lunar eclipse from many vantage points. This displays the view from the moon in dramatic fashion. The brightness ranges are somewhat compressed from what I'd consider as the realistic values. This points to consider displaying eclipse images in 16-bit format that can show greater brightness ranges in correct proportion with suitable display software.